Three Vessels

My brother gave me the following puzzle:

He didn't state the problem fully, so I looked it up online here. However, I did not look at the answer; I'm not like that. In fact, I won't look at the answer even after I answer it.

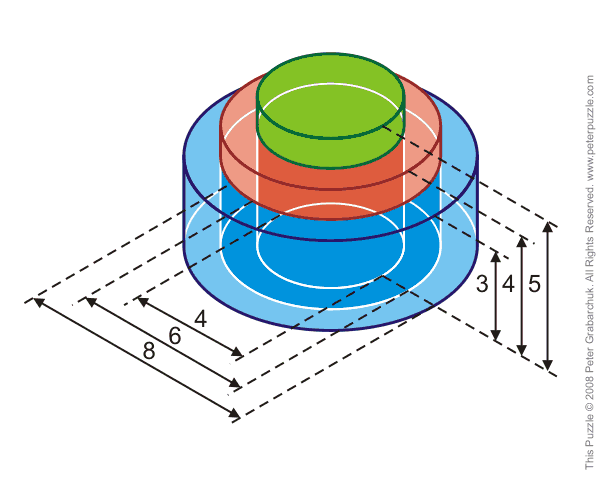
There are three vessels of different color: green, red and blue, with sizes as shown.

The green vessel is put into the red one, and the red one into the blue one.

Each vessel is full of water.

The object is to determine which vessel contains the largest quantity of water. The thickness of the walls of the vessels can be ignored.

At first, I didn't understand the problem because I was looking at it from a fully mathematical perspective (it seemed trivial). In other words, I was overlooking water displacement (the negligible wall thickness led me to think in terms of water superposition, lol).

Moreover, the feel of the puzzle seems to want to challenge intuition. So, perhaps the correct answer is that the green vessel contains the largest quantity of water, but we'll see.

With these things in mind, let's recall that the equation for the volume of a cylinder is as follows: $$ V=\pi r^2h. $$ Therefore, the blue, red and green cylinders have the following volumes, respectively: $$\begin{align} V_b&=48\pi,\\ V_r&=36\pi,\\ V_g&=20\pi. \end{align}$$ However, let's take a look at the blue cylinder; its water is being displaced by an internal cylinder of diameter $6$. Hence, its water volume is $$ \hat{V_b}=V_b-\pi3^3=21\pi. $$ Similarly, the red cylinder's water volume is $$ \hat{V_r}=V_r-\pi4^2=20\pi. $$ Finally, the green cylinder has no internal cylinder. So, it's water volume is the same as its volume; $\hat{V_g}=V_g$.

Our final results are as follows: $$\begin{align} \hat{V_b}&=21\pi,\\ \hat{V_r}&=20\pi,\\ \hat{V_g}&=20\pi. \end{align}$$ So, our counter-intuition was incorrect; the blue cylinder holds the largest amount of water.

Here is another puzzle.